Einführung
Wir betrachten ein mehrstufiges Zufallsexperiment mit den zwei Ereignissen
- $A$: Ein Schüler lernt für die Prüfung.
- $B$: Ein Schüler besteht die Prüfung.
Das Baumdiagramm habe die Gestalt
Hat ein Schüler gelernt, so besteht er mit einer Wahrscheinlichkeit von 90 % die Prüfung, hat er nicht gelernt, besteht er die Prüfung nur mit einer Wahrscheinlichkeit von 20 %. Die Wahrscheinlichkeit, dass ein Schüler die Prüfung besteht, hängt also davon ab, ob er gelernt hat. Mit anderen Worten: Die Wahrscheinlichkeit für $B$ (und auch für $\overline{B}$) hängt davon ab, ob $A$ eingetreten ist (oder nicht). Diese Wahrscheinlichkeiten der zweiten Stufe des Baumdiagramms heißen bedingte Wahrscheinlichkeiten, da für sie eine Bedingung $-$ hier $A$ oder $\overline{A}$ $-$ vorliegt. Wir verwenden die folgenden Bezeichnungen
Es ergeben sich die folgenden Interpretationen:
- $P_A(B)$ ist die Wahrscheinlichkeit, dass ein Schüler, der für die Prüfung gelernt hat, die Prüfung auch besteht.
- $P_A(\overline{B})$ ist die Wahrscheinlichkeit, dass ein Schüler, der für die Prüfung gelernt hat, die Prüfung nicht besteht.
- $P_{\overline{A}}(B)$ ist die Wahrscheinlichkeit, dass ein Schüler, der nicht für die Prüfung gelernt hat, die Prüfung dennoch besteht.
- $P_{\overline{A}}(\overline{B})$ ist die Wahrscheinlichkeit, dass ein Schüler, der nicht für die Prüfung gelernt hat, die Prüfung auch nicht besteht.
Ähnliches gilt für die Wahrscheinlichkeiten $P_B(A)$, $P_B(\overline{A})$, $P_{\overline{B}}(A)$ und $P_{\overline{B}}(\overline{A})$.
Wichtig ist die Unterscheidung zwischen $P(A\cap B)$, $P_A(B)$ und $P_B(A)$:
- $P(A\cap B)$ bezeichnet die Wahrscheinlichkeit, dass ein Schüler die Prüfung besteht und gelernt hat.
- $P_A(B)$ bezeichnet die Wahrscheinlichkeit, dass ein Schüler die Prüfung besteht, wenn er gelernt hat.
- $P_B(A)$ bezeichnet die Wahrscheinlichkeit, dass ein Schüler gelernt hat, wenn er die Prüfung besteht.
1. Info
Wenn wir Wahrscheinlichkeiten im Sachzusammenhang interpretieren möchten, müssen wir darauf achten, wie $A$ und $B$ miteinander in Beziehung stehen:
Berechnungen
Formel für die bedingte Wahrscheinlichkeit
Die Pfadmultiplikationsregel besagt, dass $P(A)\cdot P_A(B) = P(A\cap B)$. Damit folgt unmittelbar
\[P_A(B)=\frac{P(A\cap B)}{P(A)}.\]Für $P_A(B)$ ist auch die Bezeichnung $P(B|A)$ üblich. Wir nennen $P_A(B)$ die Wahrscheinlichkeit von $B$ unter der Bedingung $A$. Entsprechend gilt die Formel für andere Konstellationen, z.B. $P_B(A)=\frac{P(A\cap B)}{P(B)}$ oder $P_{\overline{A}}(B)=\frac{P(\overline{A}\cap B)}{P(\overline{A})}$.
Im Beispiel haben wir $P_A(B)=0{,}9$ und $P_{\overline{A}}(B)=0{,}2$. Die Wahrscheinlichkeit eine Prüfung zu bestehen ist also größer, wenn man gelernt hat.
Das Ganze und der Teil
Bedingte Wahrscheinlichkeiten lassen sich auch mit Hilfe relativer Häufigkeiten beschreiben. Allgemein können Wahrscheinlichkeiten als relative Häufigkeiten oder Anteile interpretiert werden:
\[\text{Wahrscheinlichkeit} = \text{Anteil} =\frac{\text{Teil}}{\text{Ganze}}.\]Angenommen in unserem Beispiel haben 200 Schüler die Prüfung geschrieben. Dann haben
- 126 Schüler $-$ oder $\frac{126}{200}=63\%$ $-$ gelernt und die Prüfung bestanden,
- 14 Schüler $-$ oder $\frac{14}{200}=7\%$ $-$ gelernt und die nicht Prüfung bestanden,
- 12 Schüler $-$ oder $\frac{12}{200}=6\%$ $-$ nicht gelernt und die Prüfung bestanden,
- 48 Schüler $-$ oder $\frac{48}{200}=24\%$ $-$ nicht gelernt und die Prüfung nicht bestanden.
Für $P_A(B)$ betrachten wir nur die Schüler, die gelernt haben, das sind $126+14=140.$ Davon haben nun $126$ die Prüfung bestanden. Wir erhalten $P_A(B)=\frac{126}{140}=90\%$.
Zusammengefasst:
- $P(A\cap B)$: Der Teil sind die Schüler, die die Prüfung bestanden und gelernt haben. Das Ganze sind alle Schüler.
- $P_A(B)$: Der Teil sind die Schüler, die die Prüfung bestanden und gelernt haben. Das Ganze sind die Schüler, die gelernt haben.
Das inverse Baumdiagramm
Es ist wichtig zu erwähnen, dass im Baumdiagramm
die Wahrscheinlichkeiten $P_B(A)$, $P_B(\overline{A})$, $P_{\overline{B}}(A)$ und $P_{\overline{B}}({\overline{A}})$ nicht abgelesen werden können. Um diese bedingten Wahrscheinlichkeiten ablesen zu können, benötigen wir $B$ und $\overline{B}$ auf der ersten und $A$ und $\overline{A}$ auf der zweiten Stufe. Mit anderen Worten: Wir müssen ein neues Baumdiagramm aufstellen, das sogenannte inverse Baumdiagramm, indem $A$ und $B$ vertauscht sind.
Dafür berechnen wir zunächst $P(B)=0{,}05+0{,}15=0{,}2$. Damit ist $P(\overline{B})=0{,}8$. Aus $P(A\cap B)=P(B)\cdot P_B(A)$ (1. Pfadendwahrscheinlichkeit des inversen Baumdiagramms) folgt dann $P_B(A)=0{,}05:0{,}2=0{,}25$. Analog berechnen wir die weiteren bedingten Wahrscheinlichkeiten.
Das inverse Baumdiagramm lautet schließlich
Hier treten nun die Wahrscheinlichkeiten mit $B$- und $\overline{B}$-Bedingung auf. Wir können z.B. ablesen, dass $P_{\overline{B}}(A)=0{,}5625$ ist. Für das Beispiel bedeutet dies: Die Wahrscheinlichkeit, dass ein Schüler, der die Prüfung nicht besteht, gelernt hat, beträgt 56,25 %.
Der Satz von Bayes
Aus der Defintion der bedingten Wahrscheinlichkeit
\[P_A(B)=\frac{P(A\cap B)}{P(A)}\]folgt $P(A\cap B)=P(A)\cdot P_A(B)$. Für die bedingte Wahrscheinlichkeit mit $A$ und $B$ vertauscht gilt dann
\[\begin{align*} P_B(A)&=\frac{P(A\cap B)}{P(B)}\\ P_B(A)&=\frac{P(A)\cdot P_A(B)}{P(B)}.\\ \end{align*}\]Mit letzterer Formel lassen sich bedingte Wahrscheinlichkeiten direkt umrechnen, sie wird auch Satz von Bayes genannt.
Im obigen Baumdiagramm gilt beispielsweise
\[\begin{align*} P_B(A)&=\frac{P(A)\cdot P_A(B)}{P(B)}\\ &=\frac{0{,}05\cdot 0{,}01}{0{,}2}\\ &=0{,}25. \end{align*}\]Stochastische Unabhängigkeit
Eng verbunden mit dem Begriff der stochastischen Unabhängigkeit ist die stochastische Unabhängigkeit. Wir erinnern an das Einführungsbeispiel mit den zwei Ereignissen
- $A$: Ein Schüler lernt für die Prüfung.
- $B$: Ein Schüler besteht die Prüfung.
und dem Baumdiagramm
Die Wahrscheinlichkeit von $B$ hängt hier davon ab, ob $A$ eingetreten ist. Wir sagen dazu auch, dass $A$ und $B$ stochastisch abhängig sind. Wäre dies nicht der Fall, hätte das Baumdiagramm also z.B. die Gestalt
so wäre die Wahrscheinlichkeit von $B$ nicht davon abhängig, ob $A$ eingetreten ist. Wir sagen dann, dass $A$ und $B$ stochastisch unabhängig sind. Mit anderen Worten: Zwei Ereignisse $A$ und $B$ sind stochastisch unabhängig, falls $P_A(B)=P_{\overline{A}}(B)$.
Auf unser Beispiel bezogen (mit dem 2. Baumdiagramm) bedeutet die stochastische Unabhängigkeit von $A$ und $B$, dass das Lernen für eine Prüfung unabhängig vom Bestehen der Prüfung ist.
Baumdiagramme und stochastische Unabhängigkeit
2. Info
Sind zwei Ereignisse $A$ und $B$ stochastisch unabhängig, so können wir diese Information beim Erstellen von Baumdiagrammen gezielt nutzen: Die beiden Wahrscheinlichkeitspaare auf der zweiten Stufe stimmen überein.
Ein Baumdiagramm mit stochastisch unabhängigen Ereignissen $A$ und $B$ habe die Gestalt

Wie lautet die Wahrscheinlichkeit 5 ? Da $A$ und $B$ stochastisch unabhängig sind gilt $P_A(B)=P_{\overline{A}}(B)$. Die Wahrscheinlichkeit 5 ist also $0{,}3$. Das restliche Baumdigramm kann nun wie gewohnt vervollständigt werden.
Haben wir ein vollständig ausgefülltes Baumdiagramm vorliegen, so können wir wie gewohnt verschiedene Wahrscheinlichkeiten bestimmen.
3. Info
Bestimmung von Wahrscheinlichkeiten anhand eines Baumdiagramms (1. Stufe A und 2. Stufe B):
Weitere Formulierungen der stochastischen Unabhängigkeit
Es gibt mehrere ähnliche Aussagen, die alle die stochastische Unabhängigkeit beschreiben. Die folgenden Aussagen sind äquivalent:
- $P_A(B)=P_{\overline{A}}(B)$
- $P(B)=P_A(B)$
- $P(A\cap B)=P(A)\cdot P(B)$
Außerdem können hier beliebig $A$ durch $\overline{A}$ und $B$ durch $\overline{B}$ ersetzt werden. Das heißt: $A$ und $B$ sind genau dann stochastisch unabhängig, falls $A$ und $\overline{B}$ (oder $\overline{A}$ und $B$ oder $\overline{A}$ und $\overline{B}$) stochastisch unabhängig sind.
Exkurs: Beweise
-
1 ist äquivalent zu 2:
Die Pfadadditionsregel besagt, dass
\[P(B)=P(A\cap B)+P(\overline{A}\cap B).\]Die Pfadmultiplikationsregel besagt, dass
\[P(A\cap B)=P(A)\cdot P_A(B)\]und
\[P(\overline{A}\cap B)=P(\overline{A})\cdot P_{\overline{A}}(B).\]Damit folgt
\[P(B) = P(A)\cdot P_A(B) + P(\overline{A})\cdot P_{\overline{A}}(B).\]Es gilt $P_A(B)=P_{\overline{A}}(B)$ genau dann, wenn
\[P(B) = P(A)\cdot P_A(B) + P(\overline{A})\cdot P_A(B).\]Es folgt
\[P(B)=(P(A)+P(\overline{A}))\cdot P_A(B).\]Da $P(A)+P(\overline{A})=1$ ist nun $P(B)=P_A(B)$.
-
2 ist äquivalent zu 3: Die Pfadmultiplikationsregel besagt, dass $P(A\cap B)=P(A)\cdot P_A(B)$. Nun gilt $P(B)=P_A(B)$ genau dann, wenn $P(A\cap B)=P(A)\cdot P(B)$.
Prüfen auf stochastische Unabhängigkeit
Um festzustellen, ob zwei Ereinisse $A$ und $B$ stochastisch abhängig oder unabhängig sind, müssen wir eine der obigen drei Formulierungen prüfen. Sind die bedingten Wahrscheinlichkeiten bekannt, weil z.B. das Baumdiagramm gegeben ist, können wir die stochastische Unabhängigkeit direkt mit der 1. Formulierung (“die Pfadwahrscheinlichkeiten der 2. Stufe sind gleich”) feststellen (siehe Beispiele oben).
Sind keine bedingten Wahrscheinlichkeiten bekannt, verwenden wir häufig die 3. Formulierung.
Beispiel: Cannabis und Amphetamine (1)
Wir betrachten die Ereignisse
- A: Eine Person konsumiert Cannabis.
- B: Eine Person konsumiert Amphetamine.
Aus Studien sei bekannt, dass $P(A)=3\%$ und $P(B)=1\%$. Außerdem gelte $P(A\cap B)=0{,}02\%$.
Sind $A$ und $B$ stochastisch unabhängig?
Es gilt $P(A)\cdot P(B)=0{,}03\cdot 0{,}01=0{,}0003$. Da $P(A\cap B)=0{,}0002\neq0{,}0003$ sind $A$ und $B$ stochastisch abhängig.
Beispiel: Romeo und Julia (1)
Die Wahrscheinlichkeit, dass beide anwesend sind, beträgt 45 %. Die Wahrscheinlichkeit, dass beide fehlen, beträgt 10 %. Die Wahrscheinlichkeit, dass Romeo anwesend ist und Julia fehlt, beträgt 15 %.
Wir betrachten die Ereignisse:
- A: Romeo ist anwesend.
- B: Julia ist anwesend.
Sind $A$ und $B$ stochastisch unabhängig?
Es gilt $P(A\cap B)=0{,}45$, $P(\overline{A}\cap \overline{B})=0{,}1$ und $P(A\cap \overline{B})=0{,}15$. Wir berechnen
\[\begin{align*} P(A) &= P(A\cap B) + P(A\cap \overline{B})\\ & = 0{,}45 + 0{,}15 \\ &= 0{,}6 \end{align*}\] \[\begin{align*} P(\overline{B}) & = P(A\cap \overline{B}) + P(\overline{A}\cap \overline{B}) \\ & = 0{,}15 + 0{,}1 \\ &= 0{,}25 \end{align*}\]Nun ist $P(A)\cdot P(\overline{B})=0{,}6 \cdot 0{,}25 = 0{,}15$. Es gilt also $P(A)\cdot P(\overline{B}) = P(A\cap \overline{B})$. Damit sind $A$ und $\overline{B}$ stochastisch unabhängig, und somit auch $A$ und $B$. (Diese Berechnungen werden mit den Begriffen des nächsten Abschnitts übersichtlicher.)
Vier-Felder-Tafeln
Neben Baumdiagrammen können Zufallsexperimente mit zwei Ereignissen auch durch Vier-Felder-Tafeln dargestellt werden. Die allgemeine Form lautet
| $B$ | $\overline{B}$ | $\Sigma$ | |
|---|---|---|---|
| $A$ | $P(A \cap B)$ | $P(A \cap \overline{B})$ | $P(A)$ |
| $\overline{A}$ | $P(\overline{A} \cap B)$ | $P(\overline{A} \cap \overline{B})$ | $P(\overline{A})$ |
| $\Sigma$ | $P(B)$ | $P(\overline{B})$ | $1$ |
Das Summenzeichen $\Sigma$ beschreibt, dass die äußeren Wahrscheinlichkeiten gleich der Summe zugehörigen inneren Wahrscheinlichkeiten sind:
- $P(A) = P(A \cap B) + P(A \cap \overline{B})$
- $P(\overline{A}) = P(\overline{A} \cap B) + P(\overline{A} \cap \overline{B})$
- $P(B) = P(A \cap B) + P(\overline{A} \cap B)$
- $P(\overline{B}) = P(A \cap \overline{B}) + P(\overline{A} \cap \overline{B})$
Diese Beobachtung ist wichtig, wenn wir Vier-Felder-Tafeln aufstellen wollen.
Beispiel: Cannabis und Amphetamine (2)
Wir hatten die Ereignisse
- A: Eine Person konsumiert Cannabis.
- B: Eine Person konsumiert Amphetamine.
Bekannt war, dass $P(A)=3\%$, $P(B)=1\%$ und $P(A\cap B)=0{,}02\%$. Damit ergibt sich
| $B$ | $\overline{B}$ | $\Sigma$ | |
|---|---|---|---|
| $A$ | $0{,}0002$ | $P(A \cap \overline{B})$ | $0{,}03$ |
| $\overline{A}$ | $P(\overline{A} \cap B)$ | $P(\overline{A} \cap \overline{B})$ | $P(\overline{A})$ |
| $\Sigma$ | $0{,}01$ | $P(\overline{B})$ | $1$ |
Die übrigen Wahrscheinlichkeiten können wie folgt berechnet werden:
- $P(\overline{A}) = 1-0{,}03 = 0{,}97$
- $P(\overline{B}) = 1-0{,}01 = 0{,}99$
- $P(\overline{A} \cap B)= 0{,}01 - 0{,}0002 = 0{,}0098$
- $P(A \cap \overline{B}) = 0{,}03 - 0{,}0002 = 0{,}0298$
- $P(\overline{A} \cap \overline{B}) = 0{,}97 - 0{,}0098 = 0{,}9602$
Damit lautet die vollständige Vier-Felder-Tafel
| $B$ | $\overline{B}$ | $\Sigma$ | |
|---|---|---|---|
| $A$ | $0{,}0002$ | $0{,}0298$ | $0{,}03$ |
| $\overline{A}$ | $0{,}0098$ | $0{,}9602$ | $0{,}97$ |
| $\Sigma$ | $0{,}01$ | $0{,}99$ | $1$ |
Hier können wir z.B. ablesen, dass eine Person mit einer Wahrschheinlichkeit von 96,02 % weder Cannabis noch Amphetamine konsumiert.
Beispiel: Romeo und Julia (2)
Wir hatten die Ereignisse
- A: Romeo ist anwesend.
- B: Julia ist anwesend.
Bekannt war $P(A\cap B)=0{,}45$, $P(\overline{A}\cap \overline{B})=0{,}1$ und $P(A\cap \overline{B})=0{,}15$. Damit ergibt sich
| $B$ | $\overline{B}$ | $\Sigma$ | |
|---|---|---|---|
| $A$ | $0{,}45$ | $0{,}15$ | $P(A)$ |
| $\overline{A}$ | $P(\overline{A} \cap B)$ | $0{,}1$ | $P(\overline{A})$ |
| $\Sigma$ | $P(B)$ | $P(\overline{B})$ | $1$ |
Die übrigen Wahrscheinlichkeiten können wie folgt berechnet werden:
- $P(A) = 0{,}45 + 0{,}15 = 0{,}6$
- $P(\overline{A}) = 1- 0{,}6 = 0{,}4$
- $P(\overline{B}) = 0{,}15 + 0{,}1 = 0{,}25$
- $P(B) = 1 - 0{,}25 = 0{,}75$
- $P(\overline{A} \cap B) = 0{,}75 - 0{,}45 = 0{,}3$
Damit lautet die vollständige Vier-Felder-Tafel
| $B$ | $\overline{B}$ | $\Sigma$ | |
|---|---|---|---|
| $A$ | $0{,}45$ | $0{,}15$ | $0{,}6$ |
| $\overline{A}$ | $0{,}3$ | $0{,}1$ | $0{,}4$ |
| $\Sigma$ | $0{,}75$ | $0{,}25$ | $1$ |
Hier können wir z.B. ablesen, dass Romeo mit einer Wahrschheinlichkeit von 60 % anwesend ist.
4. Info
Rechenregel in Vier-Felder-Tafeln:
Wir können von ‘innen nach außen addieren’: Die Summe zweier innerer Wahrscheinlichkeiten einer Zeile (bzw. Spalte) ist die Wahrscheinlichkeit in der entsprechenden letzten Zeile (bzw. Spalte). Dies kann umgeformt werden, wenn z.B. eine Wahrscheinlichkeit in der letzten Zeile (bzw. Spalte) gegeben ist.
Haben wir eine vollständig ausgefüllte Vier-Felder-Tafel vorliegen, so können wir wie verschiedene Wahrscheinlichkeiten bestimmen.
5. Info
Bestimmung von Wahrscheinlichkeiten anhand einer Vier-Felder-Tafel:
- $P(A)$ und $P(B)$ stehen in der letzten Zeile und Spalte.
- Die $\cap$-Wahrscheinlichkeiten stehen per Definition im Inneren der Tafel.
- Die $\cup$-Wahrscheinlichkeiten sind die Summe der drei zugehörigen inneren Wahrscheinlichkeiten.
Vier-Felder-Tafeln und stochastische Unabhängigkeit
Eine Formulierung der stochastischen Unabhängigkeit ist $P(A\cap B)=P(A)\cdot P(B)$. Diese Bedingung kann leicht anhand einer Vier-Felder-Tafel geprüft werden: Der innere Wert $P(A\cap B)$ ist das Produkt der entsprechenden äußeren Wahrscheinlichkeiten $P(A)$ und $P(B)$. Ist dies der Fall, so sagen wir, dass die Vier-Felder-Tafel multiplikativ ist.
6. Info
Sind zwei Ereignisse $A$ und $B$ stochastisch unabhängig, so können wir diese Information beim Erstellen von Vier-Felder-Tafeln gezielt nutzen: Wir können ‘von außen nach innen multiplizieren.’
Eine Vier-Felder-Tafel mit stochastisch unabhängigen Ereignissen $A$ und $B$ habe die Gestalt
| $B$ | $\overline{B}$ | $\Sigma$ | |
|---|---|---|---|
| $A$ | $x$ | $0{,}7$ | |
| $\overline{A}$ | |||
| $\Sigma$ | $0{,}2$ | $1$ |
Da $A$ und $B$ stochastisch unabhängig sind, ist die Vier-Felder-Tafel mutiplikativ, und es gilt $P(A\cap B)=P(A)\cdot P(B)$. Die Wahrscheinlichkeit $x$ ist also $0{,}2\cdot 0{,}7=0{,}14$. Die restliche Vier-Felder-Tafel kann nun wie gewohnt vervollständigt werden.
Haben wir eine vollständig ausgefüllte Vier-Felder-Tafel vorliegen, können wir sie interpretieren. Um dabei festzustellen, ob $A$ und $B$ stochastisch unabhägig sind, müssen wir prüfen, ob die Vier-Felder-Tafel multiplikativ ist.
Beispiel: Cannabis und Amphetamine (3)
Die Vier-Felder-Tafel hatte die Gestalt
| $B$ | $\overline{B}$ | $\Sigma$ | |
|---|---|---|---|
| $A$ | $0{,}0002$ | $0{,}0298$ | $0{,}03$ |
| $\overline{A}$ | $0{,}0098$ | $0{,}9602$ | $0{,}97$ |
| $\Sigma$ | $0{,}01$ | $0{,}99$ | $1$ |
Wir erkennen, dass $0{,}03 \cdot 0{,}01 \neq 0{,}0002$ ist. Die Vier-Felder-Tafel ist nicht multiplikativ, und $A$ und $B$ sind stochastisch abhängig.
Beispiel: Romeo und Julia (3)
Die Vier-Felder-Tafel hatte die Gestalt
| $B$ | $\overline{B}$ | $\Sigma$ | |
|---|---|---|---|
| $A$ | $0{,}45$ | $0{,}15$ | $0{,}6$ |
| $\overline{A}$ | $0{,}3$ | $0{,}1$ | $0{,}4$ |
| $\Sigma$ | $0{,}75$ | $0{,}25$ | $1$ |
Wir erkennen, dass $0{,}6 \cdot 0{,}75 = 0{,}45$ ist. Die Vier-Felder-Tafel ist multiplikativ, und $A$ und $B$ sind stochastisch unabhängig.
7. Info
Bestimmung von bedingten Wahrscheinlichkeiten anhand einer Vier-Felder-Tafel:
- Bedingte Wahrscheinlichkeiten müssen mit Formeln der Art $P_B(A)=\frac{P(A\cap B)}{P(B)}$ berechnet werden.
- $A$ und $B$ sind stochastisch unabhängig, wenn die Vier-Felder-Tafel multiplikativ ist.
Vergleich: Baumdiagramme und Vier-Felder-Tafeln
Baumdiagramme und Vierfeldertafeln stellen Wahrscheinlichkeiten, die beim Betrachten von zwei Ereignissen auftreten, auf unterschiedliche Weise dar. In Baumdiagrammen lassen sich die einzelnen Stufen eines Zufallsexperiments gut nachvollziehen: Zunächst tritt das Ereignis $A$ ein, anschließend das Ereignis $B$. Dabei können bedingte Wahrscheinlichkeiten wie $P_A(B)$ direkt abgelesen werden. Vierfeldertafeln hingegen behandeln die Ereignisse $A$ und $B$ symmetrisch. Sowohl $P(A)$ als $P(B)$ sind direkt aus den Tabellenwerten ersichtlich.
| \( B \) | \( \overline{B} \) | \( \Sigma \) | |
|---|---|---|---|
| \( A \) | |||
| \( \overline{A} \) | |||
| \( \Sigma \) |
Weitere Aufgaben
Stehen weder ein Baumdiagramm noch eine Vierfeldertafel zur Verfügung, können wir mit den vorgestellten Formeln arbeiten. Dabei kann es jedoch hilfreich sein, sich das Baumdiagramm oder die Vierfeldertafel gedanklich vorzustellen.
8. Info
Formel-Übersicht:
- Satz von der Gegenwahrscheinlichkeit:
- Satz von Sylvester:
- Formel für die bedingte Wahrscheinlichkeit:
- Zerlegungssatz:
9. Info
Formel-Übersicht und Lösungsstrategie, wenn zwei der Wahrscheinlichkeiten $P(A)$, $P(B)$, $P(A\cup B)$ und $P(A\cap B)$ gegeben sind und stochastische Unabhängigkeit vorliegt:
- Satz von der Gegenwahrscheinlichkeit:
- Satz von Sylvester:
- Formel für die bedingte Wahrscheinlichkeit bei stochastischer Unabhängigkeit:
- Zerlegungssatz:
- Stochastische Unabhängigkeit:
Venn-Diagramme
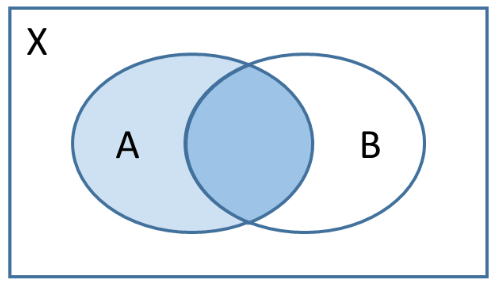
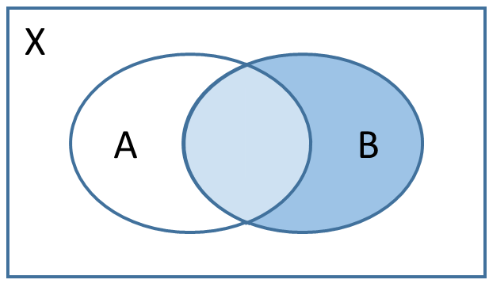
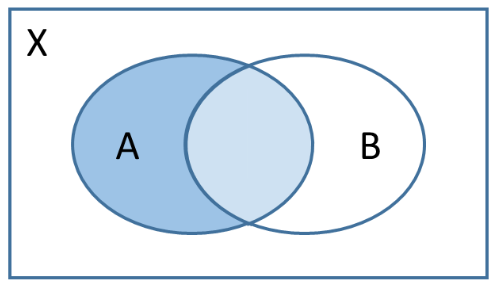
Bedingte Wahrscheinlichkeiten können auch in Venn-Diagrammen dargestellt werden. Das Ereignis, auf das die jeweilige Bedingung nicht zutrifft, wird weiß gefärbt. Das dunkle Blau bezeichnet den Teil, das dunkle zusammen mit dem hellen Blau das Ganze:
| $P_A(B)$ | $P_B(\overline{A})$ | $P_A(\overline{B})$ |
|---|---|---|
 |
 |
 |
10. Info
Venn-Diagramme mit bedingten Wahrscheinlichkeiten:
Das helle und das dunkle Blau bilden zusammen die Bedingung. Füllen das helle und dunkle Blau die ganze Fläche aus, gibt es also keine einschränkende Bedingung.